|
PGSuper 6.1
Precast-prestressed Girder Bridges
|
|
PGSuper 6.1
Precast-prestressed Girder Bridges
|
In 2008, TxDOT initiated Project 0-6374 to investigate prestress losses in pretensioned concrete girders. The final report from the project included new prestress loss provisions that were found to be simpler, more conservative, and more precise than the current methods outlined within the AASHTO LRFD Bridge Design Specifications. A reference to the report is below:
"Effect of New Prestress Loss Estimates on Pretensioned Concrete Bridge Girder Design"; David Garber, Jose Gallardo, Dean Deschenes, David Dunkman, and Oguzhan Bayrak; Report No. FHWA/TX-12/0-6374-2; October 2012, Rev. June 2013, Published August 2013
This method has been implemented in PGSuper and can be selected via the Project Criteria library Losses tab. The table below is a summary of the loss equations recommended in the report. Refer to the report and the rest of this document for more details.

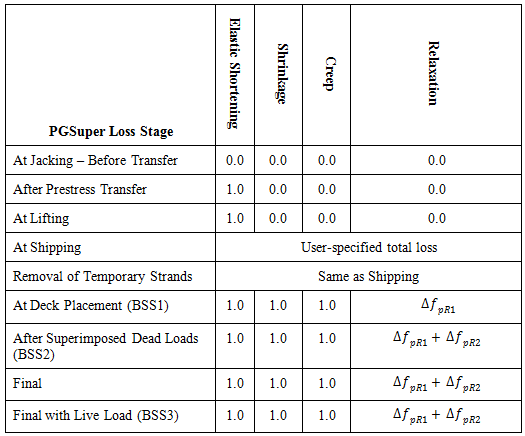
The TxDOT loss method only computes loss values at jacking, prestress release, and at final. However, losses are required at all defined intermediate stages. The table below lists the fraction of each loss component that is applied in these intermediate stages.
For elastic shortening at release, the TxDOT 0-6374-2 method assumes a strand stress at release of 0.70 fpu. The method also assumes that the elastic shortening loss can be computed at mid-girder and is constant along the length of the girder. These assumptions drastically simplify evaluation since iteration is not required, and the losses must only be computed at one location along the girder. The research claims that this method is not only easier to implement, but generates more accurate results than other refined methods.
The equations for elastic shortening along the entire girder are as follows:
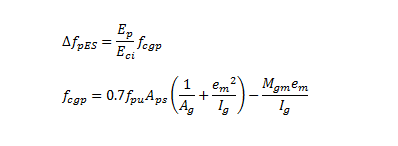
Where:
Note that Dfcdp is computed in a similar manner for use in creep loss evaluation.
The 0.70 fpu assumption described above is sensible for low-relaxation strands at normal (e.g., 0.75 fpu) jacking stresses. However, stress-relieved strands and user-input jacking forces can be defined in the bridge model which means that virtually any jacking stress is possible. Also, the research database appears only to consider prismatic precast I-beams with common prestressing configurations: beams with temporary strands, debonding, or arrangements with strands above the beam neutral axis were not considered. In these cases, the 0.7 fpu assumption could result in incorrect or even negative losses. In order to accommodate for this possibility, and to allow TxDOT engineers to experiment with different methods for computing fcgp, three different options are provided:
Note: It is TxDOT policy not to consider shipping during design, however this loss method may be used by other agencies or consultants where shipping is a consideration.
Shipping occurs at an unknown time between release and deck placement and there is no way to compute time-dependent losses for the new method, even if the time of shipping is known accurately. Therefore, users must define the time-dependent loss at shipping using a lump sum value, or a percentage of the total final time-dependent prestress loss. Checking will not be performed to insure that this value is realistic.