|
PGSuper
3.1
Precast-prestressed Girder Bridges
|
|
PGSuper
3.1
Precast-prestressed Girder Bridges
|
Time-dependent material properties are computed using the AASHTO LRFD, ACI 209R-92, and CEB-FIP 1990 models.
AASHTO does not define a time-dependent model for concrete compressive strength. The ACI 209R-92 model is used.
Modulus of elasticity is defined by a modified version of LRFD Equation 5.4.2.4-1. See Concrete Properties for details.
Shrinkage strain is defined by a modified version of LRFD Equation 5.4.2.3.3-1. See Concrete Properties for details.
Creep coefficient is defined by a modified version of LRFD Equation 5.4.2.3.2-1. See Concrete Properties for details.
AASHTO does not define an intrinsic model for strand relaxation. The ACI 209R-92 model is used.
Compressive strength is computed by ACI 209R-92 Equation 2-1.
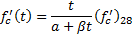
From ACI 209R-92 Table 2.2.1
| Type of Curing | Cement Type | a | b |
|---|---|---|---|
| Moist | I | 4.0 | 0.85 |
| Moist | III | 2.3 | 0.92 |
| Steam | I | 1.0 | 0.95 |
| Steam | III | 0.7 | 0.98 |
Modulus of elasticity is computed by ACI 209R-92 Equation 2-5.
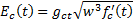
for gct = 33.0,
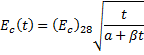
Shrinkage strain is computed by ACI 209R-92 Equations 2-7, 2-9, 2-10, 2-15, 2-16, and 2-22. Here we present the shrinkage strain as an ultimate shrinkage value multiplied by modification factors.
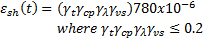
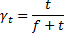
f = 35 for moist cured concrete (ACI Eqn. 2-9) and 55 for steam cured concrete (ACI Eqn. 2-10).
t = shrinkage duration
gcp = 1.0 for steam curing.
From ACI 209R-92 Table 2.5.3
| Moist Curing Duration (days) | gcp |
|---|---|
| 1 | 1.2 |
| 3 | 1.1 |
| 7 | 1.0 |
| 14 | 0.93 |
| 28 | 0.86 |
| 90 | 0.75 |
gcp is linearly interpolated for other curing durations.
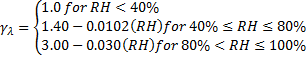
RH = Average Ambient Relative Humidity
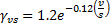
v/s = volume to surface ratio
Creep coefficient is computed by ACI 209R-92 Equations 2-8, 2-11, 2-12, 2-14, and 2-21. Here we present the creep coeficient as an ultimate coefficient value multiplied by modification factors.
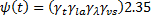
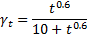
t = time after loading (days)
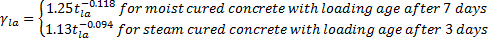
tla is the age of the concrete at the time of loading (days)
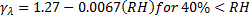
RH = Average Ambient Relative Humidity
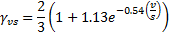
v/s = volume to surface ratio
Relaxation is computed from the equations given in ACI 209R-92 Table 3.7.1.
| Strand Type | Relaxation |
|---|---|
| Stress Relieved | 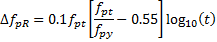
|
| Low Relaxation | 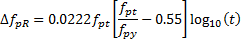
|
The concrete compressive strength is computed by CEB-FIP 1990 Eqn. 2.1-53.
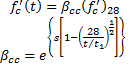
| Cement Type | s |
|---|---|
| Rapid Hardening High Strength (RS) | 0.20 |
| Normal Hardening (N) | 0.25 |
| Rapid Hardening (R) | 0.25 |
| Slowly Hardening (SL) | 0.38 |
The modulus of elasticity is computed by CEB-FIP 1990 Eqn. 2.1-57.
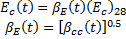
Shrinkage strain is computed by CEB-FIP 1990 Equation 2.1-74.
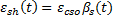
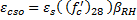
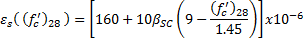
| Cement Type | bsc |
|---|---|
| Rapid Hardening High Strength (RS) | 8 |
| Normal Hardening (N) | 5 |
| Rapid Hardening (R) | 5 |
| Slowly Hardening (SL) | 4 |
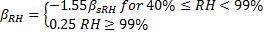
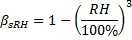
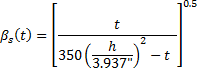
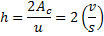
Creep coefficient is computed by CEB-FIP 1990 Equation 2.1-64.
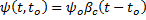
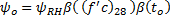
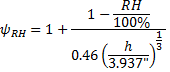
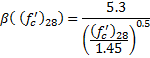
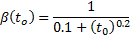
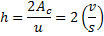
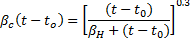
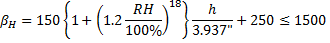
Relaxation is defined in CEB-FIP 2.3.4.5. For design purposes, the relxation lossses in CEB-FIP Figure 2.3.3 can be used. The curves in this figure have been fit into the following format