|
PGSplice 8.0
Precast-prestressed Spliced Girder Bridges
|
|
|
PGSplice 8.0
Precast-prestressed Spliced Girder Bridges
|
|
PGSuper and PGSplice can provide an accurate computation of bearing seat elevations and other bearing geometry information based on input bridge geometry. The figures in the section describe how bearing locations are computed.
The following figure shows a plan view at a generic girder/pier intersection. 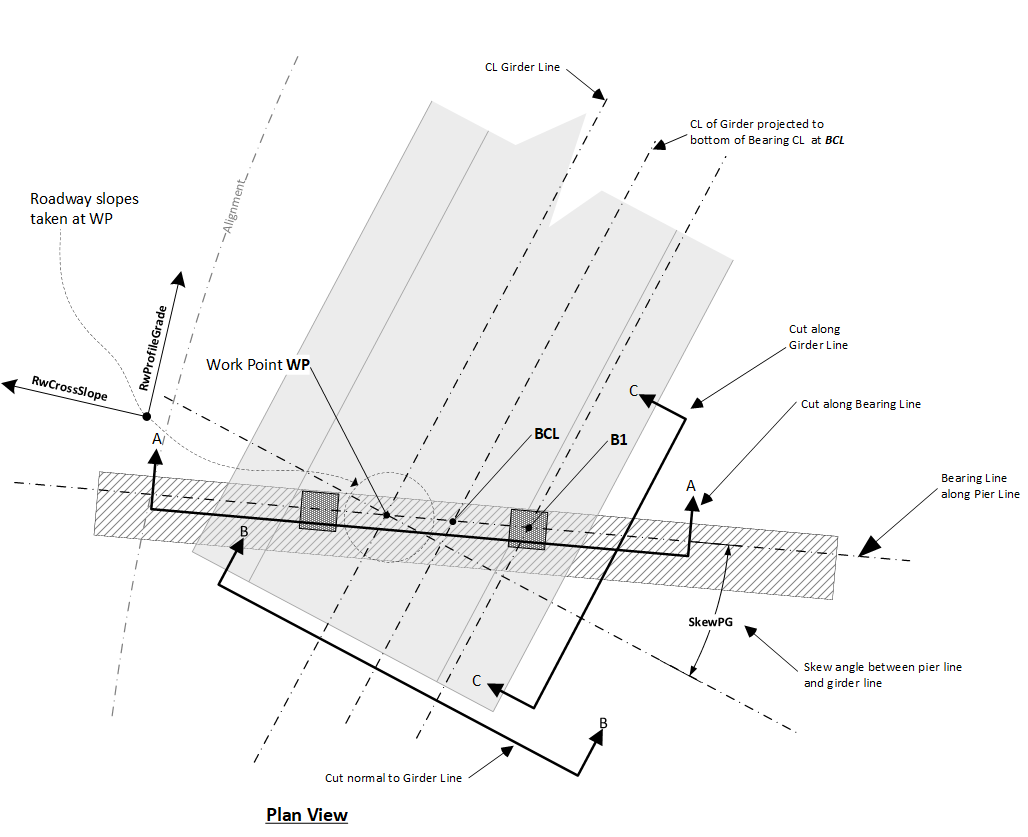
The figure below shows a section view cut along the Pier Line (Section A-A). Note that bearing spacing is laid out along the bearing line from the BCL location as shown in the figure. From this, there are a couple of observations that should be noted:
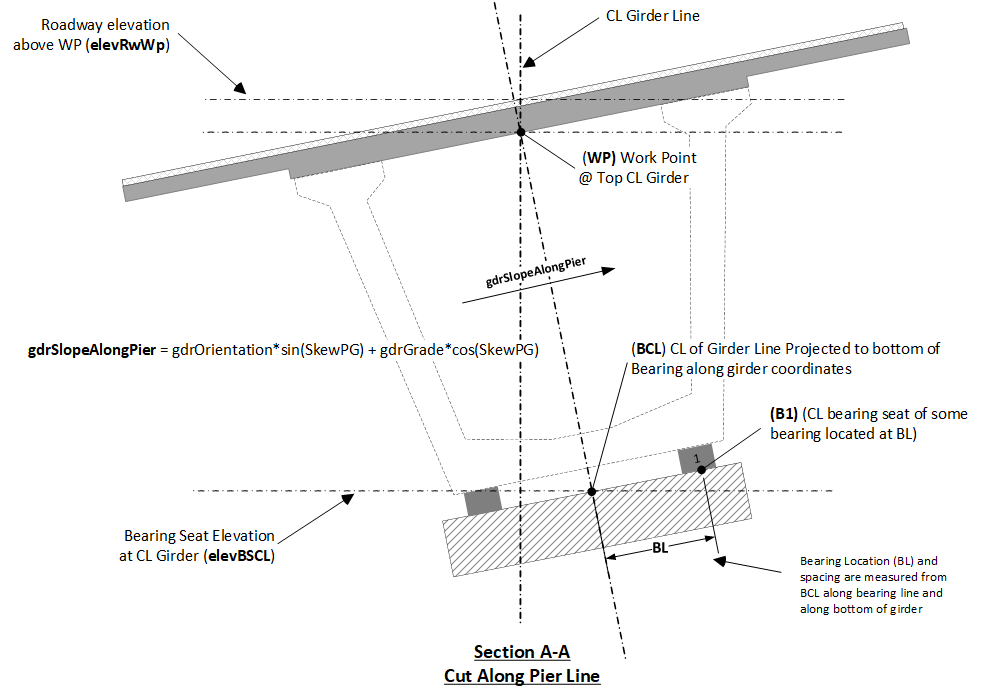
The figure below shows section cuts normal to (Section B-B) and along the girderline (Section C-C). 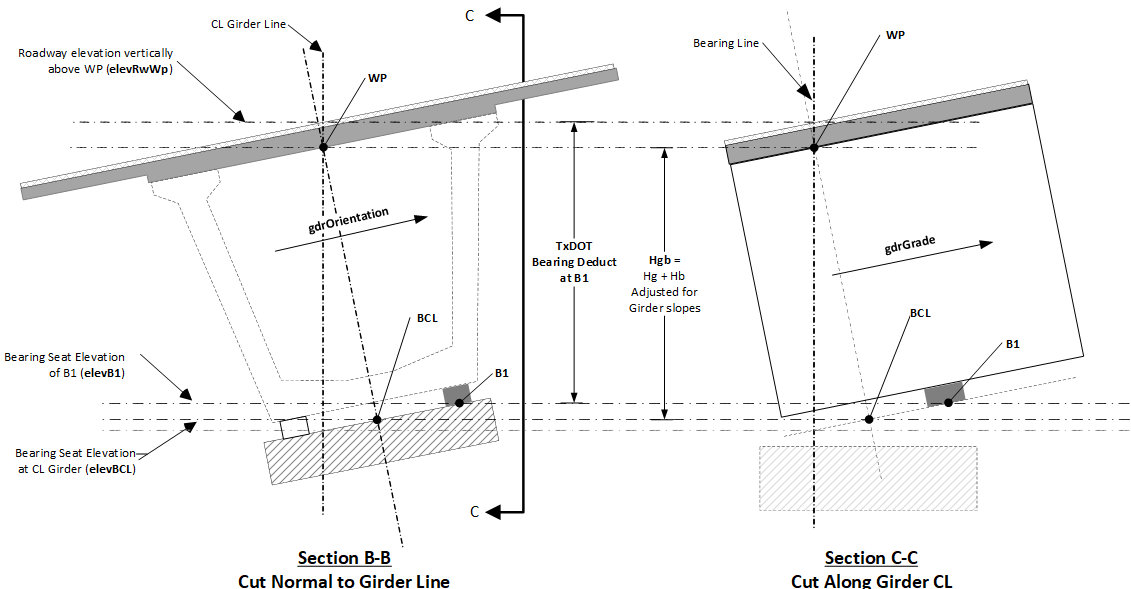
The plan view point coincident with B1 is located as shown in the figure below. 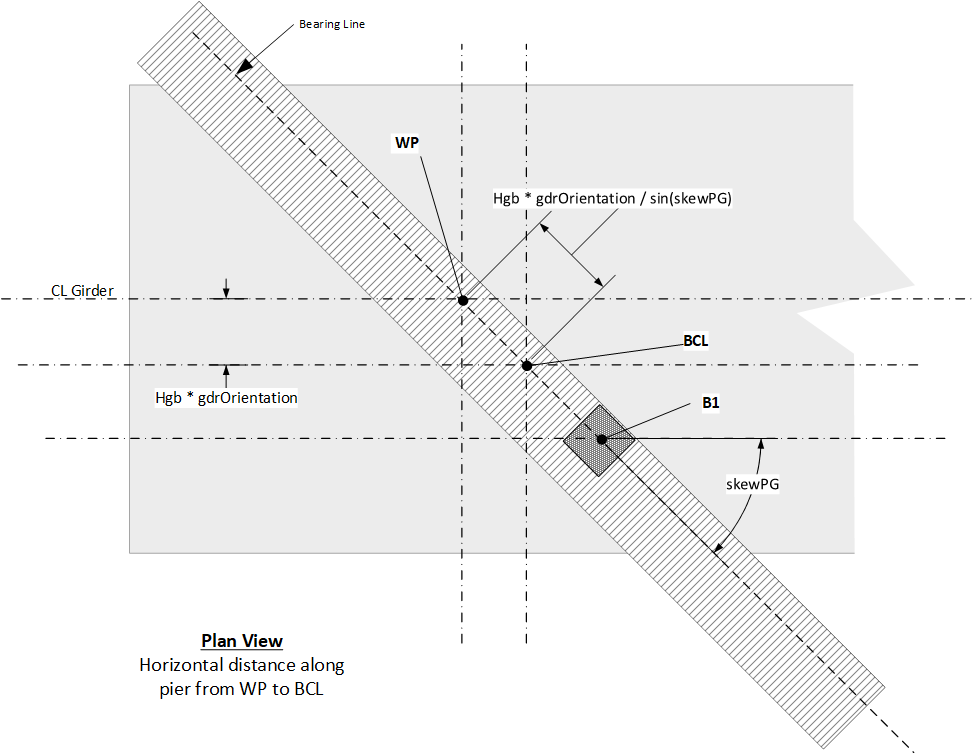
The station, offset, and roadway surface elevation are computed for this point. The bearing seat elevation is then computed as
\[ elev_{B1} = elevRW_{B1} - H_{gb} \]
where
\( elev_{B1}\) = top of bearing elevation
\( elevRW_{B1} \) = roadway surface elevation above center point of bearing B1
\( H_{gb} = (H_g + H_b)/( cos(gdrOrientation) cos(gdrGrade) ) \)
\( H_g \) = height of girder
\( H_b \) = thickness of bearing